Summary
AlaskaFWANT-Vs2019 (Yang & Gao, 2020 ) is a 3-D shear-wave isotropic model for Alaska and western Canada from full-wave ambient noise tomography with resolvable depth for the top 150 km.
Quicklinks
Description
| Name | AlaskaFWANT-Vs2019 |
| Title | 3-D shear-wave isotropic model for Alaska and western Canada from full-wave ambient noise tomography |
| Type | 3-D Tomography Earth Model |
| Sub Type | Shear-wave velocity (km/s) |
| Year | 2019 |
| Data Revision | r.0.0 (revision history) |
| Short Description | AlaskaFWANT-Vs2019 is a 3-D shear-wave isotropic model for Alaska and western Canada from full-wave ambient noise tomography with resolvable depth for the top 150 km. The Vs model with good resolution (> 70% recovery) is from the depth of 15 km to the depth of 110 km. The tomography was based on an empirical Green’s function data set extracted from cross-correlation between station pairs. The tomography method involves 3-D wave propagation simulation. The travel-time different between the synthetics and the observed empirical Green’s functions are inverted for finite-frequency sensitivity kernels to get velocity perturbations. The velocity model is updated iteratively for a total of five iterations. |
| Authors: | Xiaotao Yang:
Department of Geosciences, University of Massachusetts Amherst. Amherst, MA 01003 |
| Previous Model | None |
| Reference Model | The reference velocity model consists of two parts: a global shear-velocity model for the top 400 km (Shapiro and Ritzwoller, 2002 ) and the IASP91 1-D Earth model from 400 km down to 1000 km (Kennett and Engdahl, 1991 ). |
| Model Download | YangAndGao-AlaskaFWANT-Vs2019-0.0.nc (see metadata ), is the netCDF 3 Classic file for the model. |
| Model Homepage | |
| Depth Coverage | From 0 km to 150 km |
| Area | Alaska (United States) and western Canada (latitude: 56° to 66.8°, longitude: -160.991° to -136.519°) |
| Data Set Description | The data set includes the shear velocity model on an inversion grid of longitude and latitude with spacing of 0.05° in both directions. No smoothing or interpolation applied. Vertical grid spacing increases with depth. |
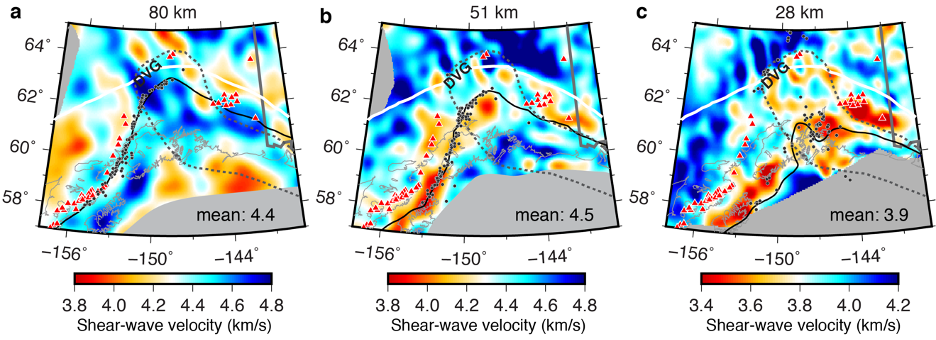
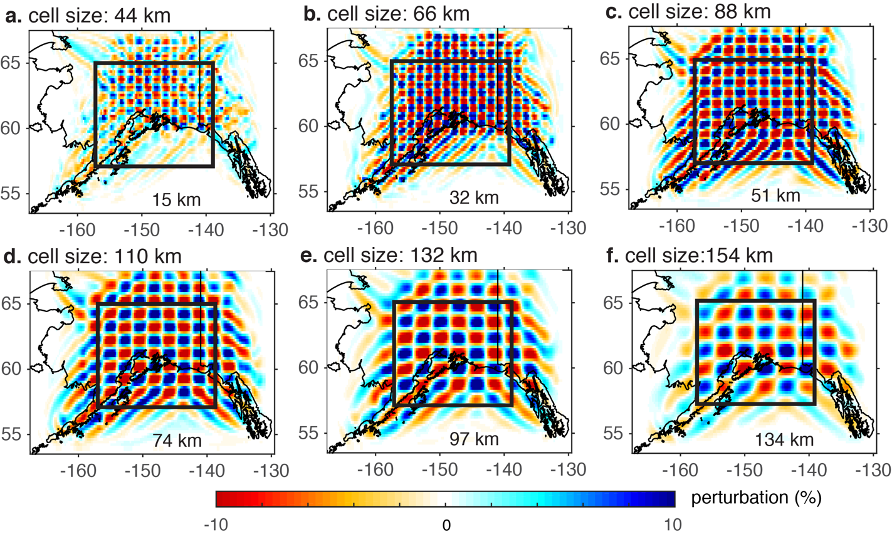
| Model Resolution | As tested and validated by previous applications of full-wave tomographic imaging (e.g., Gao, 2018; Zhang and Shen, 2008 ), Rayleigh waves are most sensitive to P-wave velocity at shallow depths (< 15 km) and to S-wave velocity at greater depths. Although P-wave velocity model is also provided for all depth, interpretation of P velocities deeper than 15 km and shallower than 5 km is discouraged. The model provided here (Figure 1) is from the inversion result of the 5th iteration without smoothing or interpolation. When interpreting the velocity model, it is recommended that the user smooth the model based on the best resolution at the corresponding depth, as shown in (Yang & Gao, 2020 ) and Figure 2 on this page. The checkerboard tests show that shear-wave velocity perturbations can be well resolved with horizontal scales of 44 km, 66 km, 88 km, 110 km, 132 km, and 154 km at the depths of 15 km, 32 km, 51 km, 74 km, 97 km, and 134 km, respectively. |
Citations and DOIs
To cite the original work behind this Earth model:
- Yang, X., H. Gao (2020). Segmentation of the Aleutian-Alaska subduction zone revealed by full-wave ambient noise tomography: implications for the along-strike variation of volcanism, Journal of Geophysical Research-Solid Earth, https://doi.org/10.1029/2020JB019677
To cite IRIS DMC Data Products effort:
- Trabant, C., A. R. Hutko, M. Bahavar, R. Karstens, T. Ahern, and R. Aster (2012), Data Products at the IRIS DMC: Stepping Stones for Research and Other Applications, Seismological Research Letters, 83(5), 846–854, https://doi.org/10.1785/0220120032.
DOI for this EMC webpage: https://doi.org/10.17611/dp/emc.2020.alaskafwantvs.1
References
- Shapiro, N. M., and M. H. Ritzwoller (2002), Monte-Carlo inversion for a global shear-velocity model of the crust and upper mantle, Geophys. J. Int., 151(1), 88-105, https://doi.org/10.1046/j.1365-246X.2002.01742.x
- Kennett, B. L. N., Engdahl, E. R. Traveltimes for global earthquake location and phase identification. Geophys. J. Int., 105: 429-465 (1991)
- Zhang, Z., Shen, Y. Cross-dependence of finite-frequency compressional waveforms to shear seismic wave speeds. Geophys. J. Int., 174(3): 941-948 (2008)
- Gao, H. Three-dimensional variations of the slab geometry correlate with earthquake distributions at the Cascadia subduction system. Nat. Commun.,9:(2018)
Credits
- r.0.0 model provided by Xiaotao Yang.
Revision History
revision r.0.0: uploaded November 4, 2020.
Timeline
- 2020-11-04
- online






