Summary
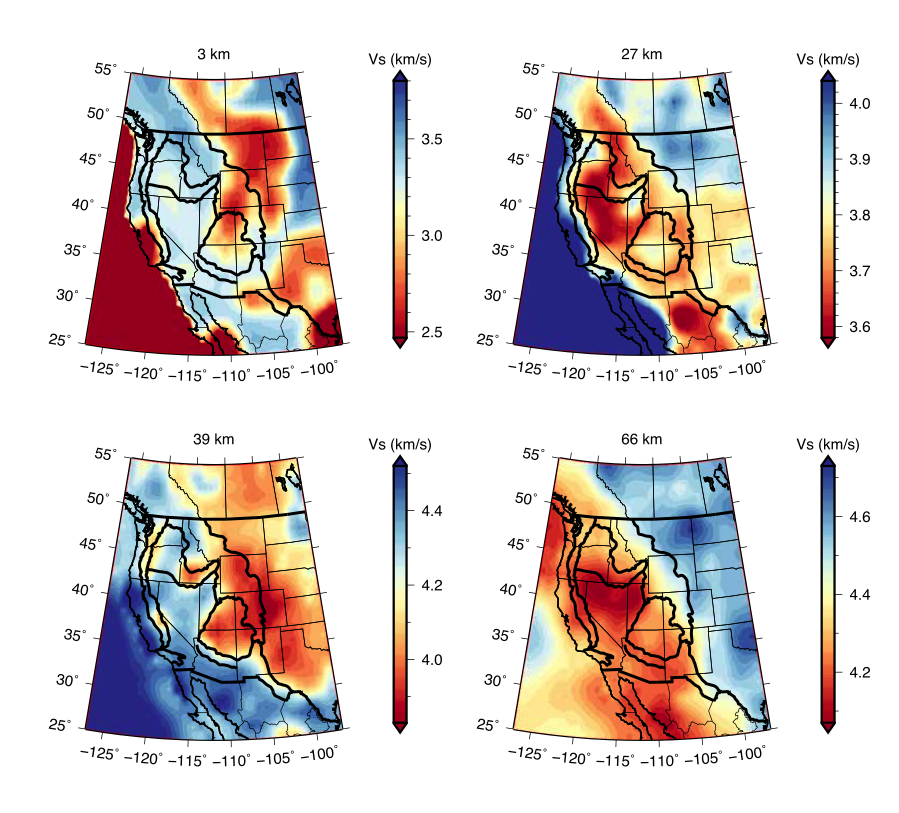
WUS-CAMH-2015 (Chai, Ammon, Maceira, and Herrmann, 2015) is a shear velocity model that combines spatially interpolated/smoothed receiver functions, surface-wave dispersion and gravity observations through a 3D simultaneous inversion to image the subsurface S-wave velocity structure of the western U.S. region.
Quicklinks
Description
| Name | WUS-CAMH-2015 |
| Title | 3D shear-wave velocity model of the western United States |
| Type | 3-D Tomography Earth Model |
| Sub Type | Shear-wave velocity (km/s) |
| Year | 2015 |
| Short Description | The WUS-CAMH-2015 shear velocity model combines spatially interpolated/smoothed receiver functions, surface-wave dispersion and gravity observations through a 3D simultaneous inversion to image the subsurface S-wave velocity structure of the western U.S. region. Data include 3608 interpolated P-wave receiver functions, 900 Rayleigh-wave group velocity dispersion curves, and wavenumber filtered Bouguer gravity observations. Constrained by simplified receiver functions and multiple geophysical observations, the velocity model is a reliable starting point for more detailed seismic investigations. Supplements to the original manuscript (available from AGU) include the original-formatted model along with Python and Fortran tools for extracting pieces of the model. |
| Authors: | |
| Chengping Chai | |
| Department of Geosciences | |
| Pennsylvania State University | |
| University Park, PA, 16802, USA | |
| Charles J. Ammon | |
| Department of Geosciences | |
| Pennsylvania State University | |
| University Park, PA, 16802, USA | |
| Monica Maceira | |
| Los Alamos National Laboratory | |
| Los Alamos, NM, 87545, USA | |
| Robert B. Herrmann | |
| Department of Earth and Atmospheric Sciences | |
| Saint Louis University | |
| St. Louis, MO, 63108, USA | |
| Previous Model | None |
| Reference Model | None |
| Model Download | |
| The above model expressed as shear velocity in km/s. Density (g/cm3) and P-wave velocity (in km/s) are also provided, which are inferred based on the imperial relationship between density and shear wave velocity (Maceira and Ammon, 2009) and Vp/Vs ratios from Crust 1.0 (Laske et al., 2013): WUS-CAMH-2015.nc (see metadata ), is the netCDF file for the model |
|
| Depth Coverage | 0 to 2048 km |
| Area | Western U.S. region (latitude: 25°/55°, longitude: -127°/-97°) |
| Data Set Description | [Chai et al. (2015)] The dataset includes spatially interpolated/smoothed P-wave receiver functions from ~1000 stations, Rayleigh-wave group velocities (short periods from Herrmann et al., 2013 and long periods from Ekström, 2011), and wavenumber filtered Bouguer gravity observations (Balmino et al., 2012). |
| Supplemental Information | The supplemental information page for this model contains images comparing single-station averaged receiver functions with spatially interpolated/smoothed receiver functions, clustering analysis results of the WUS-CAMH-2015 3D shear wave velocity model, synthetic tests of receiver function interpolation, applications of receiver function interpolation for smaller seismic arrays, and an animation of different time slices of receiver functions. |
Citations and DOIs
To cite the original work behind this Earth model:
- Chai, C., C. J. Ammon, M. Maceira, and R. B. Herrmann (2015), Inverting interpolated receiver functions with surface wave dispersion and gravity: Application to the western U.S. and adjacent Canada and Mexico, Geophysical Research Letters, 42(11), 4359-4366, https://doi.org/10.1002/2015GL063733.
To cite IRIS DMC Data Products effort:
- Trabant, C., A. R. Hutko, M. Bahavar, R. Karstens, T. Ahern, and R. Aster (2012), Data Products at the IRIS DMC: Stepping Stones for Research and Other Applications, Seismological Research Letters, 83(5), 846–854, https://doi.org/10.1785/0220120032.
DOI for this EMC webpage:
References:
Balmino, G., N. Vales, S. Bonvalot, and A. Briais (2012), Spherical harmonic modelling to ultra-high degree of Bouguer and isostatic anomalies, J. Geod., 86(7), 499–520, https://doi.org/10.1007/s00190-011-0533-4.
Ekström, G. (2011), A global model of Love and Rayleigh surface wave dispersion and anisotropy, 25–250 s, Geophys. J. Int., 187(3), 1668–1686, https://doi.org/10.1111/j.1365-246X.2011.05225.x.
Herrmann, R. B., C. J. Ammon, and H. Benz (2013), Group velocity dispersion for North America. [Available at http://www.eas.slu.edu/eqc/eqc_research/NATOMO.]
Laske, G., G. Masters, Z. Ma, and M. Pasyanos (2013), Update on CRUST1.0—A 1-degree global model of Earth’s crust, Abstracts EGU2013-2658 presented at 2013 EGU General Assembly Conference, Vienna, Austria, 7–12 April.
Maceira, M., and C. J. Ammon (2009), Joint inversion of surface wave velocity and gravity observations and its application to central Asian basins shear velocity structure, J. Geophys. Res., 114, B02314, https://doi.org/10.1029/2007JB005157.
Credits
Model provided Chengping Chai
Timeline
- 2016-06-27
- online






