Data Services Products: EMC-KEA20 Radially anisotropic shear wave velocity model for East Asia

Summary

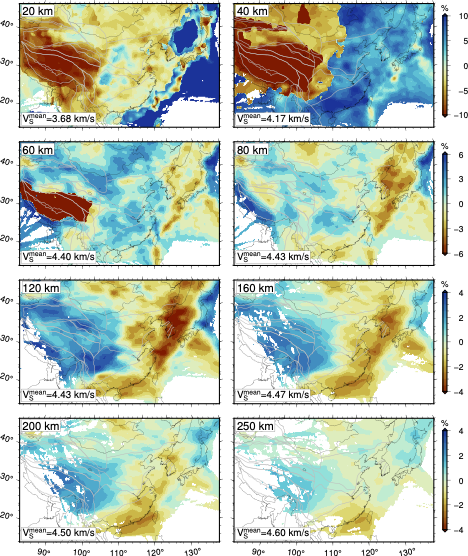
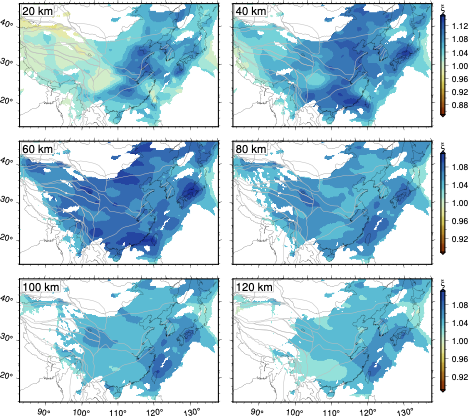
KEA20 is a radially anisotropic model for the crust and mantle of East Asia derived from earthquake and ambient noise surface wave dispersion constraints in the period range 5-375 s including fundamental and overtone mode branches. The tomographic model is constructed using a local sensitivity kernel approach with respect to a reference 3-D model. Isotropic velocities are resolvable down to the mantle transition zone, while radial anisotropy is resolved down to approximately 120 km depth. Here, we provide absolute values for VSV, VSH, and Moho depth for both our tomographic model and the reference model.

Description

Name KEA20
Title Radially anisotropic shear wave velocity model for East Asia
Type 3-D Tomography Earth Model
Sub Type Radially anisotropic S velocities (km/s) and Moho depth (km)
Year 2021
Data Revision r0.0 (revision history)
 
Short Description   KEA20 is a radially anisotropic model for the crust and mantle of East Asia derived from earthquake and ambient noise surface wave dispersion constraints in the period range 5-375 s including fundamental and overtone mode branches. The tomographic model is constructed using a local sensitivity kernel approach with respect to a reference 3-D model. Isotropic velocities are resolvable down to the mantle transition zone, while radial anisotropy is resolved down to approximately 120 km depth. Here, we provide absolute values for VSV, VSH, and Moho depth for both our tomographic model and the reference model.
 
Authors: Michael Witek, Department of Geophysics, Kangwon National University, Chuncheon, Republic of Korea

Sung-Joon Chang, Department of Geophysics, Kangwon National University, Chuncheon, Republic of Korea

Do Yoon Lim, Earthquake and Volcano Research Division, Korea Meteorological Administration, Seoul, Republic of Korea,

Shuoxian Ning, School of Earth and Space Sciences, Peking University, Beijing, China

Jieyuan Ning, School of Earth and Space Sciences, Peking University, Beijing, China
 
Previous Model None
 
Reference Model The reference model consists of a bilinearly interpolated CRUST1.0 (Laske et al., 2013) placed on top of the AK135 mantle (Kennett et al., 1995).
 
Model Download KEA20.r0.0.nc (see metadata) model,
KEA20-Moho.r0.0.nc (see metadata) model moho depth relative to a mean Earth radius of 6371 km,
KEA20-reference-model.r0.0.nc (see metadata) reference model,
in netCDF 3 Classic format.
Model Homepage None
 
Depth Coverage 0-660 km
 
Area East Asia, Longitude: 70° E to 150° E, Latitude: 15° N to 51° N
 
Data Set Description The dataset used to create KEA20 includes 268,888 Rayleigh and 69,147 Love wave dispersion curves from previously published studies (Ritzwoller and Levshin, 1998; Visser et al., 2008; Ekström, 2011; Ritsema et al., 2011; Ma et al., 2014; You and Chang, 2017; Min and Chang, 2017; Lim and Chang, 2018; Witek et al., 2018), as well as 299,193 Rayleigh and 116,029 Love wave dispersion curves newly measured from ambient noise and earthquake waveforms. We include fundamental and overtones up to the 5th mode branch. The period range is 5-375 s. For a more detailed description of the dataset please see Table 1 in Witek et al. (2021).
 
 

Voigt averaged shear wave velocity
Figure 1. Voigt averaged shear wave velocity. Depth for each panel is indicated in the upper left corner. Colors represent percent perturbations with respect to the mean velocity denoted in the bottom left corner of each panel. The color scale for each row is shown at right. Light gray lines indicate major tectonic terranes.

Radial anisotropy parameter
Figure 2. Radial anisotropy parameter ξ=V_SH^2/V_SV^2. Depth for each panel is indicated in the upper left corner. Colors represent absolute ξ values, with the corresponding color scale for each row shown at left.

Citations and DOIs

To cite the original work behind this Earth model:

  • Witek, M., Chang, S.-J., Lim, D. Y., Ning, S., & Ning, J. (2021). Radial anisotropy in East Asia from multimode surface wave tomography. Journal of Geophysical Research: Solid Earth, 126, e2020JB021201. https://doi.org/10.1029/2020JB021201

To cite IRIS DMC Data Products effort:

  • Trabant, C., A. R. Hutko, M. Bahavar, R. Karstens, T. Ahern, and R. Aster (2012), Data Products at the IRIS DMC: Stepping Stones for Research and Other Applications, Seismological Research Letters, 83(5), 846–854, https://doi.org/10.1785/0220120032.

DOI for this EMC webpage: https://doi.org/10.17611/dp/emc.2021.kea20.1

References

  • Ekström, G. (2011). A global model of Love and Rayleigh surface wave dispersion and anisotropy, 25–250 s. Geophysical Journal International, 187, 1668–1686. https://doi.org/10.1111/j.1365-246X.2011.05225.x

  • Kennett, B. L. N., Engdahl, E. R., & Buland, R. (1995). Constraints on seismic velocities in the Earth from traveltimes. Geophysical Journal International, 122, 108-124. https://doi.org/10.1111/j.1365-246X.1995.tb03540.x

  • Laske, G., Masters, G., Ma, Z., & Pasyanos, M. (2013). Update on CRUST1.0 – A 1-degree global model of Earth’s crust. Geophysical Research Abstracts, 15 (EGU2013-2658).

  • Lim, D., & Chang, S.-J. (2018). Three-dimensional S-wave velocity structure and radial anisotropy of crust and uppermost mantle beneath East Asia. Geophysics and Geophysical Exploration, 21(1), 33–40. https://doi.org/10.7582/GGE.2018.21.1.033

  • Ma, Z., Masters, G., Laske, G., & Pasyanos, M. (2014). A comprehensive dispersion model of surface wave phase and group velocity for the globe. Geophysical Journal International, 199, 113–135. https://doi.org/10.1093/gji/ggu246

  • Min, K., & Chang, S.-J. (2017). 3D SH-wave velocity structure of East Asia using Love-wave tomography and implication on radial anisotropy. Geophysics and Geophysical Exploration, 20(1), 25–32. https://doi.org/10.7582/GGE.2017.20.1.025

  • Ritsema, J., Deuss, A., van Heijst, H. J., & Woodhouse, J. H. (2011). S40RTS: a degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophysical Journal International, 184, 1223–1236. https://doi.org/10.1111/j.1365-246X.2010.04884.x

  • Ritzwoller, M. H., & Levshin, A. L. (1998). Eurasian surface wave tomography: Group velocities. Journal of Geophysical Research, 103(B03), 4839–4878. https://doi.org/10.1029/97JB02622

  • Visser, K., Trampert, J., & Kennett, B. L. N. (2008). Global anisotropic phase velocity maps for higher mode Love and Rayleigh waves. Geophysical Journal International, 172, 1016–1032. doi: https://doi.org/10.1111/j.1365-246X.2007.03685.x

  • Witek, M., van der Lee, S., Kang, T.-S., Chang, S.-J., Ning, J., & Ning, S. (2018). S velocity model of East Asia from a cluster analysis of localized dispersion. Journal of Geophysical Research: Solid Earth, 123. https://doi.org/10.1029/2018JB016060

  • You, S.-H., & Chang, S.-J. (2017). 3D SV-wave velocity structure of East Asia using Rayleigh-wave tomography. Geophysics and Geophysical Exploration, 20(1), 12–17. https://doi.org/10.7582/GGE.2017.20.1.012

Credits

  • r0.0 model provided by Michael Witek.

Revision History

revision r0.0: uploaded June 2, 2021.

Timeline

2021-06-03
online

Contact

Categories

Tags

Earth Models Shear Wave Velocity EMC tomography Moho tomographic model CRUST1.0 Anisotropic

Related Content

These other pages were tagged similarly:

SAGE Facility has been certified as a trustworthy data repository by the CoreTrustSeal Standards and Certification Board
23:00:34 v.22510d55