Summary
Earthquake energy and rupture durations are estimated following all earthquakes with initial magnitude above Mw 6.0 and a GCMT moment tensor. The method follows Convers and Newman, 2011. These are fully automated and not reviewed by a human.
Quicklinks
Description
Much like seismic moment, the cumulative seismic energy released by an earthquake is a fundamental parameter controlled by the amount of material displaced, and the speed by which the action occurs. While the seismic moment is a measure of the amount of work performed, irrespective of speed, earthquake energy is a measure of the kinetic energy released through seismic waves during an event. While energy is proportional to moment for most earthquakes, when an event ruptures more rapidly or more slowly than expected, its energy release will differ, in some cases by an order of magnitude [Newman and Okal, 1998].
Earthquakes with fast ruptures release substantially more energy than expected given their seismic moment, hence much more strong shaking would be expected, meaning such events pose higher risks to nearby populations [e.g.Feng et al., 2010]. Conversely, for events with very slow ruptures, energy dissipation can be quite low and will be more drawn out [Convers and Newman, 2011]. Such events occur predominantly in the shallowest portions of the subduction megathrust interface, often creating anomalously large tsunami [Polet and Kanamori, 2000], and have been termed "tsunami earthquakes" for this reason [Kanamori, 1972].
The products reported here are the automated solutions of the per-station and cumulative energy release for global earthquakes with initial magnitude above Mw 6.0 and a GCMT moment tensor. Results include broadband and high-frequency data from vertical-component seismograms recorded at teleseismic distances (25° ≤ Δ ≤ 80°).
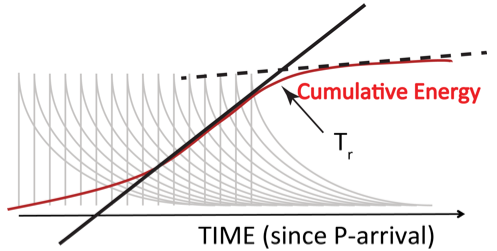
Cumulative energy
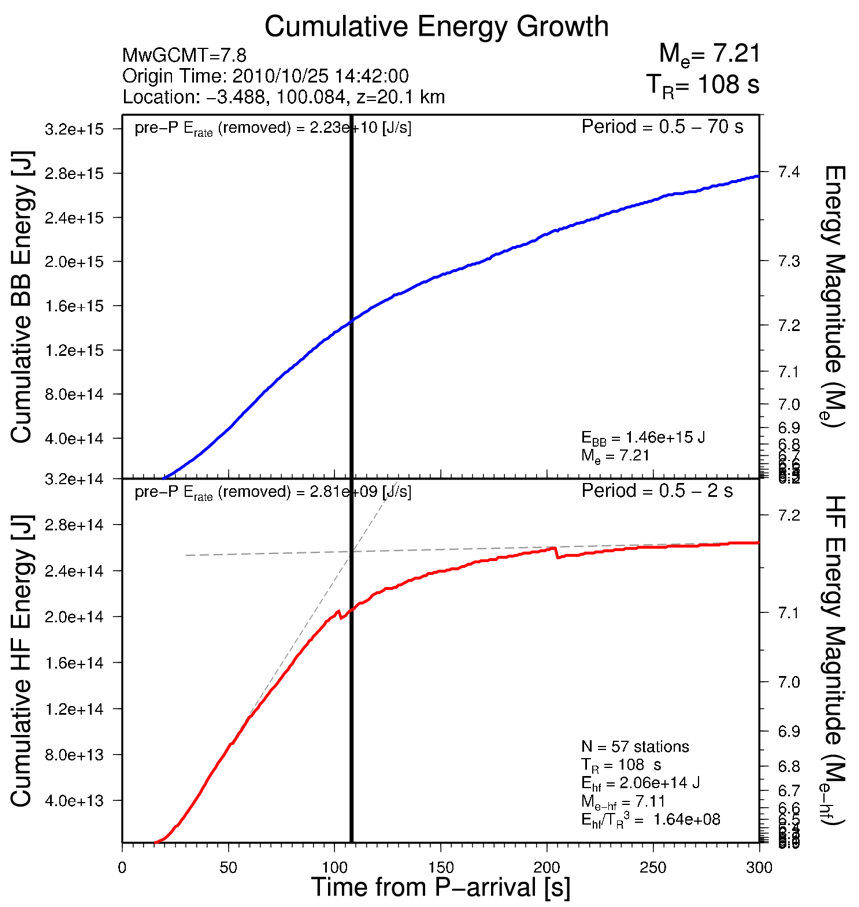
For each earthquake, cumulative energy plots at high frequency (0.5 – 2 s) and broadband range (0.5 – 70 s) are generated for a stack of available stations (57 in the example below) aligned relative to the theoretical onset of the P-arrival. The inflection point as determined by the cross-over between a near constant growth and later high-frequency energy marks the approximate rupture duration (solid vertical black line at 108s). At this point the cumulative energy is determined for both high frequency (Ehf = 2.06e14 J), and broadband (EBB = 1.46e15 J). The energy can be converted into an energy magnitude following Me=2/3 Log10E(BB)-2.9 as described by Choy and Boatwright [1995]. The high-frequency energy magnitude is equivalent and assumes only 1/5th the energy is available in that higher selected band pass.
Stations used
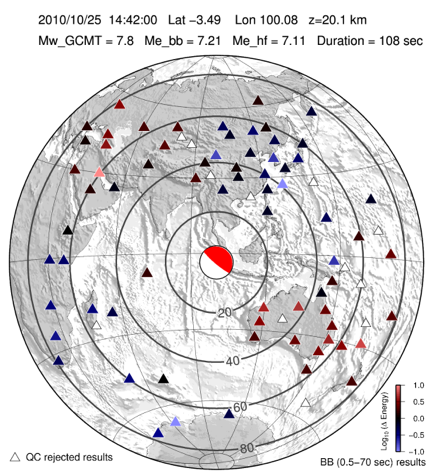
Each event includes a hemispheric visualization of the stations used for the calculations along with each stations individual deviation from the stacked average energy, calculated as log10(Estation/Eaverage). Stations are routinely used at distances greater than 25° and less than 80°. These are done to avoid near-field triplication and non-vertical take-off angles in the near field, and high-attenuation and core diffraction in the far field. The initial station set is desampled from available broadband stations by using a minimum interstation distance of 5 degrees in order to avoid bias from a dense set of stations (e.g. in California). GSN stations are given higher priority. A minimum of 8 stations meeting the QCing criteria are required for events to be published in SPUD.
Calculations of Radiated Energy
Using velocity seismograms of the P-wave group (P+pP+sP) [Boatwright and Choy, 1986; Newman and Okal, 1998] , the energy is calculated at teleseismic stations. These calculations are produced for the radiated seismic energy in increasing time windows [Convers and Newman, 2011].
Data selection
We select the vertical component of teleseismic broadband stations located between 25° and 80° of the source epicenter. Teleseismic waveforms are used to avoid triplication effects within the crust, and obtain near-vertical arrivals (thus only the vertical component is necessary). By excluding waveforms beyond 80° we avoid path contamination and heterogeneous attenuation near the core.
Data processing
Energy at the station
At individual seismic stations we calculate the energy flux from the P-wave group at that station, ε*gP, using:
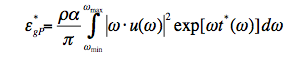
where α and ρ are the P-wave velocity and density at the receiver, and u(ω) is the frequency-dependent ground displacement corrected for instrument response [Okal, 1992]. The solution, ε*gP, determined in the frequency-domain, is not the true station energy, because it is corrected for generalized frequency-dependent attenuation, t*.
Energy at the source
To scale results from the station back to the source, we correct for: – Geometric spreading – Partitioning of energy at the source between P and S waves. – Orientation relative to the focal sphere (provided by GCMT).
The radiated energy at the earthquake source E is then:
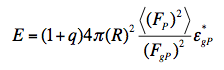
where q (= 15.6) is the relative partitioning between the S and P waves [Boatwright and Fletcher, 1984], R is the distance-dependent geometric spreading coefficient, ⟨(Fp)2⟩ (= 4/15) is the average squared radiation pattern of the direct P-wave [Aki and Richards, 1980] and Fgp is the mechanism-dependent radiation coefficient of the P-wave group including pP and sP [Boatwright and Choy].
Earthquake duration from energy
Using the above-described methods for calculating energy, we calculate E for incrementally increasing time-windows (+1 s) to calculate the cumulative growth only in at high-frequency (0.5 to 2 Hz) to avoid significant contamination by later reflected phases which tend to have most energy at long-periods. Details are described in Convers and Newman [2011].
To determine an earthquake's approximate duration, two linear regression fits are calculated, one for each the near-constant growth period excited by finite rupture, and the near-constant die-off period excited by crustal scattering and some later arrivals. The crossover point between the linear regressions, called the cross-over time Tr, approximates the maximum decay in energy growth, and is a good rapid approximation for rupture duration for large shallow earthquakes. Estimation of the slope of the growth period can be sensitive to the width of the time window over which it is estimated and result in overestimated rupture durations. To minimize this sensitivity, the window width is varied and the width yielding the minimum rupture duration is used.
Caveat Emptor
Deep earthquakes
Two issues are present for deep earthquakes:
1) The attenuation correction used in these calculations are for shallow earthquakes where the direct (P) and depth phases (pP and sP) all travel twice through along similar paths. However for deeper earthquakes, the depth phases become distinctly separated from the direct arrival, and are preferentially attenuated because those waves travel twice through the source-side crust, while the direct P takes no passes through the source-side crust.
2) Because the depth phases arrive much later than the direct P for deep earthquakes, the duration reported may be artificially lengthened. Alternatively, the algorithms may estimate duration based just on the direct P. This duration is more accurate, but again, the ultimate energy determination may be inaccurate.
Small earthquakes
For events smaller than about Mw 6.0, the energy gathered at teleseismic distances may be buried in the noise at frequencies where calculations are made. Secondly, the travel-time difference between the direct and depth phases becomes large relative to the rupture duration and can overestimate rupture duration (e.g. adding approximately 15 s to events at 30 km depth).
Early aftershocks
While the energy algorithms work well for most events, there are instances where the calculations of energy from early aftershocks or doublets may yield unrealistically high energies due to the contribution of the first event's later arrivals, namely surface waves.
Complex ruptures
Because the method relies on the cumulative development of energy through an earth that scatters energy, the energy results are comparable to highly smoothed integrated source-time functions. For events that start with a weaker initial sub-event that is separated significantly in time (e.g. the 2001/11/14 Kunlun China earthquake), the duration estimates may be blind to the pause and yield a seemingly excessive duration. Should an event start very strongly, but have a long tail with considerably less energetic rupture, the event may underestimate the true rupture duration. As a note however, in post priori tests of the 2004 MW 9.15 Sumatran earthquake, this was not an issue.
References
Aki, K., and P. G. Richards (1980), Quantitative Seismology: Theories and Methods, W.H. Freeman and Company, San Francisco.
Boatwright, J., and J. B. Fletcher (1984), The Partition of Radiated Energy Between P-wave and S-wave, Bull. Seismol. Soc. Amer., 74(2), 361-376.
Boatwright, J., and G. L. Choy (1986), Telsesismic estimates of the energy radiated by shallow earthquakes, Journal of Geophysical Research-Solid Earth and Planets, 91(B2), 2095-2112.
Choy, G. L., and J. L. Boatwright (1995), Global patterns of radiated seismic energy and apparent stress, J. Geophys. Res.-Solid Earth, 100(B9), 18205-18228.
Convers, J. A., and A. V. Newman (2011), Global Evaluation of Large Earthquake Energy from 1997 Through mid-2010, J. Geophys. Res., 116.
Feng, L. J., A. V. Newman, G. T. Farmer, P. Psimoulis, and S. C. Stiros (2010), Energetic rupture, coseismic and post-seismic response of the 2008 M-W 6.4 Achaia-Elia Earthquake in northwestern Peloponnese, Greece: an indicator of an immature transform fault zone, Geophysical Journal International, 183(1), 103-110.
Kanamori, H. (1972), Mechanism of Tsunami Earthquakes, Physics of the Earth and Planetary Interiors, 6, 346-359.
Newman, A. V., and E. A. Okal (1998), Teleseismic estimates of radiated seismic energy: The E/M0 discriminant for tsunami earthquakes, Journal of Geophysical Research, 103(B11), 26885-26898.
Okal, E. A. (1992), Use of the mantle magnitude m(m) for the reassessment of the moment of historical earthquakes .1. shallow events, Pure and Applied Geophysics, 139(1), 17-57.
Polet, J., and H. Kanamori (2000), Shallow subduction zone earthquakes and their tsunamigenic potential, Geophysical Journal International, 142(3), 684-702.
Citations and DOIs
To cite the IRIS DMC Data Products effort:
- Hutko, A. R., M. Bahavar, C. Trabant, R. T. Weekly, M. Van Fossen, T. Ahern (2017), Data Products at the IRIS‐DMC: Growth and Usage, Seismological Research Letters, 88, no. 3, https://doi.org/10.1785/0220160190.
To cite the IRIS DMC EQEnergy data product, or reference use of its repository:
- IRIS DMC (2013), Data Services Products: EQEnergy Earthquake energy & rupture duration, https://doi.org/10.17611/DP/EQE.1.
To cite the methods used for the EQEnergy data product:
- Convers, J. A., A. V. Newman (2011), Global Evaluation of Large Earthquake Energy from 1997 Through mid-2010, J. Geophys. Res., 116, B08304, https://doi.org/10.1029/2010JB007928.
To reference the use of a particular EQEnergy:
– select the EQEnergy of interest
– click on Citations to obtain its DOI
– insert the DOI in below reference:
- IRIS DMC (2013), Data Services Products: EQEnergy Earthquake energy & rupture duration, doi:INSERT DOI HERE.
Credits
- Jamie Convers, Andrew Newman & Alexander Hutko
Timeline
- 2013-12-01
- EQEnergy online at IRIS
Contributors
Jamie Convers
Georgia Tech
Andrew Newan
Georgia Tech






