Question
What is a "count" in timeseries data?
When I download data from ws-timeseries like this:
The data is returned in “counts”:
TIMESERIES IU_ANMO_00_BHZ_M, 200 samples, 20 sps, 2010-02-27T06:30:00.019538, TSPAIR, INTEGER, COUNTS 2010-02-27T06:30:00.019538 -47237 2010-02-27T06:30:00.069538 -47304 2010-02-27T06:30:00.119538 -47367 2010-02-27T06:30:00.169538 -47430 2010-02-27T06:30:00.219538 -47499 2010-02-27T06:30:00.269538 -47572 2010-02-27T06:30:00.319538 -47653
How does this translate into Earth units?
Answer
“Counts” is the raw number read off the physical instrument, ie. the voltage read from a sensor.
Like any physical instrument, a seismometer cannot measure every motion with perfect accuracy. Its responsiveness depends mainly on the frequency of motion being measured, generally represented by a Bode plot:
As demonstrated by the plot, converting to Earth units is not a simple calculation but can depend on a number of factors including the frequency of motion being measured. In other words, it is an interpretation of the data, which is something for the researcher (not the data center) to decide.
Tools for converting units
- SAC
- See the transfer command. This generally uses a SAC Poles and Zeros file containing the instrument response metadata.
- ObsPy
- ObsPy can read and write a variety of formats and perform instrument correction.
ws-timeseries
This is an alternative way of fetching data, that can be useful for single requests.
The IRIS ws-timeseries service has an internal option to perform this conversion while extracting the data:
The additional parameters are:
scale=AUTO (or Correction: “Apply Total Sensitivity” on the ws-timeseries builder) to perform the conversion to Earth units.
demean=true (or Remove mean: true on the ws-timeseries builder) to correct the zero value (see below).
Manual (nominal) conversion
The full instrument metadata documents the performance envelope of the instrument in as much detail as possible, and should be used for any serious analysis.
But for something like a simple visualization, an approximate solution may suffice:
| Simple scaling factor | Full instrument correction |
|---|---|
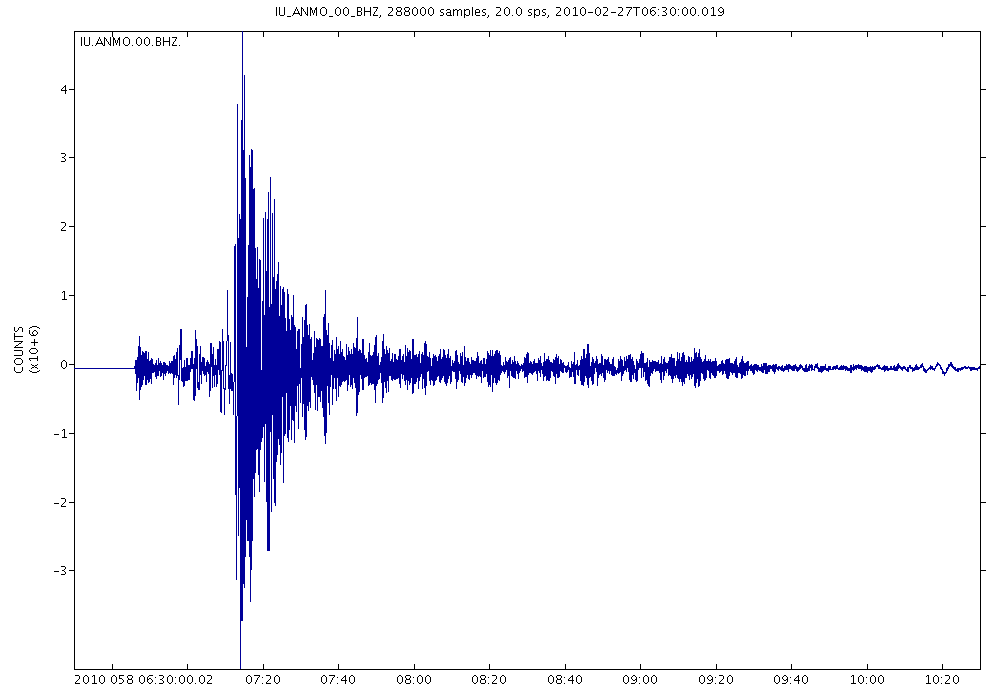 |
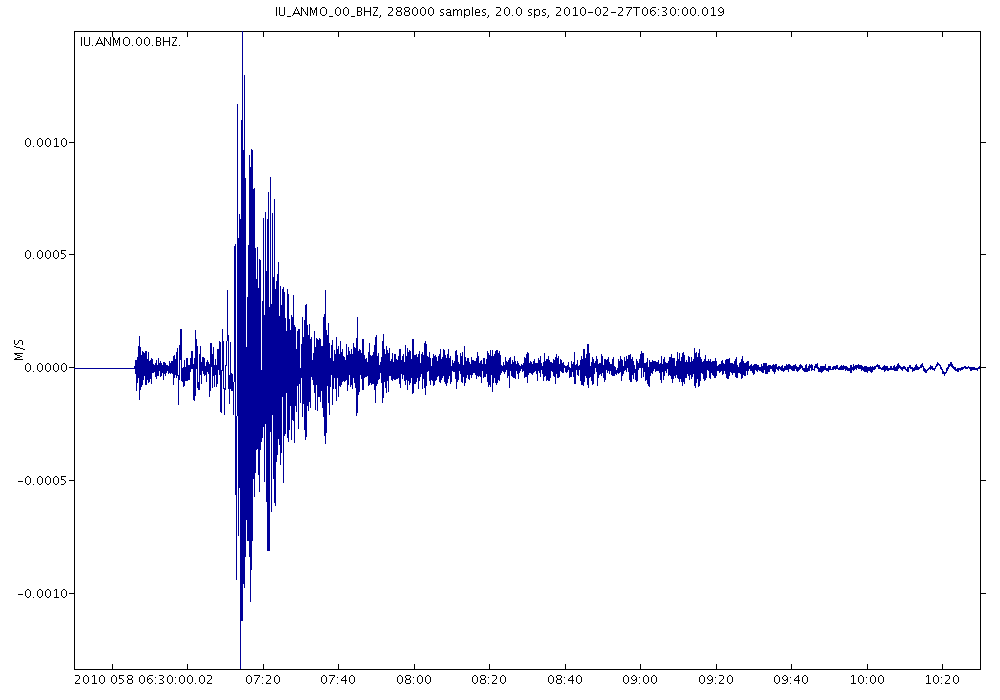 |
In this case, the instrument defines a nominal scaling factor, which can be retrieved from the FDSN ws-station service.
This requires the Network, Station, Location, Channel, and date range (can usually be just the day) for the data. In the example above, these would be:
net: IU
sta: ANMO
loc: 00
cha: BHZ
starttime: 2010-02-27
endtime: 2010-02-27
Also include in the request:
format: text
level: channel
This returns:
#Network | Station | Location | Channel | Latitude | Longitude | Elevation | Depth | Azimuth | Dip | SensorDescription | Scale | ScaleFreq | ScaleUnits | SampleRate | StartTime | EndTime IU|ANMO|00|BHZ|34.945981|-106.457133|1671.0|145.0|0.0|-90.0|Geotech KS-54000 Borehole Seismometer|3.27508E9|0.02|M/S|20.0|2008-06-30T20:00:00|2011-02-18T19:11:00
The relevant information appears several columns in:
... | Scale | ScaleFreq | ScaleUnits | SampleRate | ... ... |3.27508E9|0.02|M/S|20.0| ...
so
Scale : 3.27508E9 counts = 1 unit
ScaleFreq : 0.02 Hz = this is the frequency at which the scale is accurate
ScaleUnits : 1 unit = 1 M/S (meter/second)
SampleRate: 20.0 samples/sec
So a “count” value of 3.27508e9 would indicate ground motion of 1 m/s — you can divide the count value by 3.27508e9 to convert into meters per second.
Processing line 1 of the data…
2010-02-27T06:30:00.019538 -47237
(-47237 / 3.27508e9) = -1.4423e-5 m/s
And line 2…
2010-02-27T06:30:00.069538 -47304
(-47304 / 3.27508e9) = -1.4444e-5 m/s
Note the second line is .05s (more or less) after the first, because the data is measured at 20 samples/second. The data file gives the exact time of the measurement, but in many cases this is an unnecessary level of precision, and the header (and the ws-station data) already indicate the sample rate. In that case, you can use output=ascii1 which gives only the measurement values and not the timestamp. This reduces the data size by about 80%.
Demeaning
The raw data also doesn’t calibrate the zero-point of the instrument — in the first few seconds of data in the example above, the values are all offset by -50000 or so. Demeaning takes the mean across a timeperiod and subtracts it from each value, so that the data is “centered” at zero, which may suffice for some purposes.






