Data Services Products: EMC-nz_atom_north_chow_etal_2021_vp+vs New Zealand Adjoint TOMography velocity model (North Island)

Summary

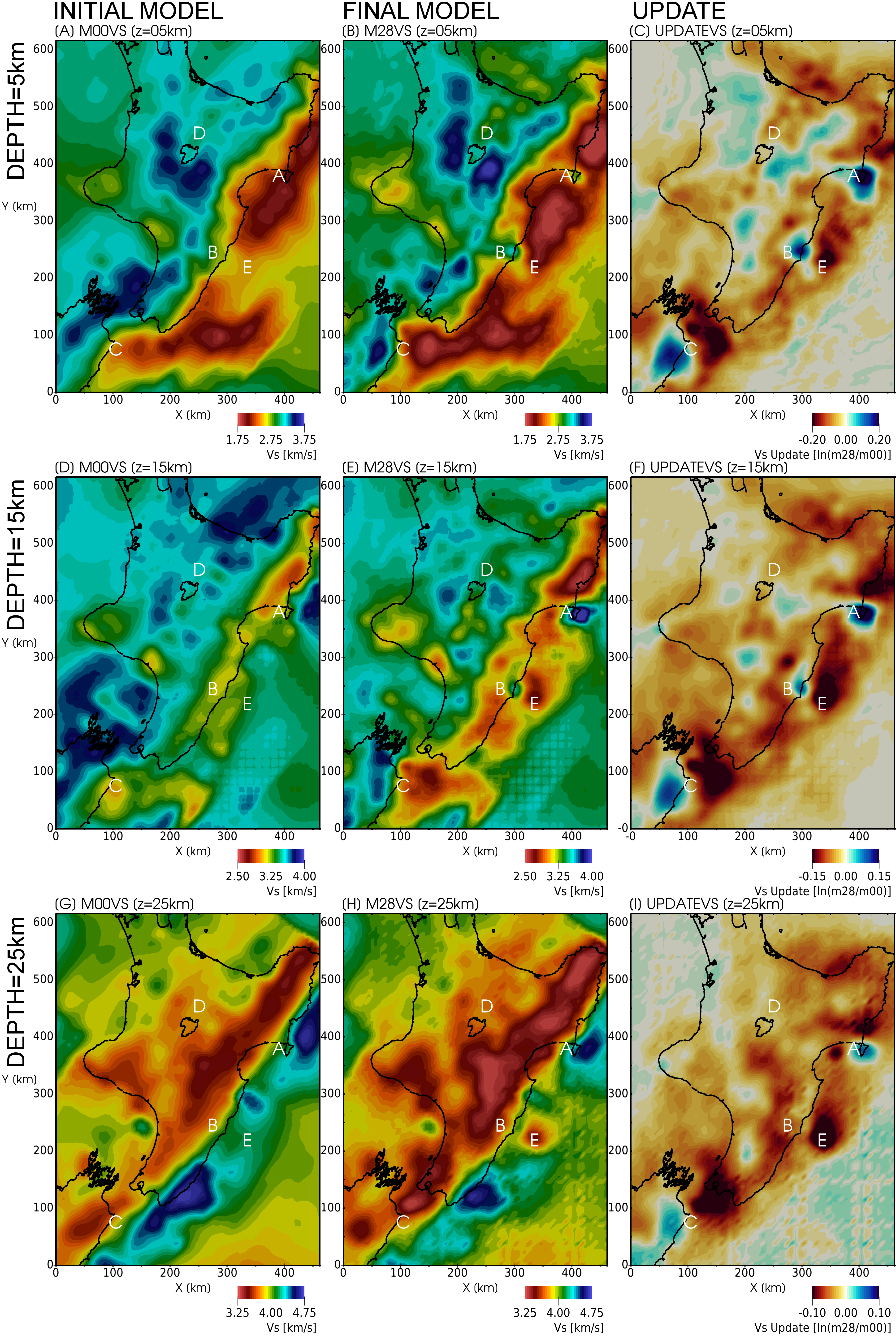
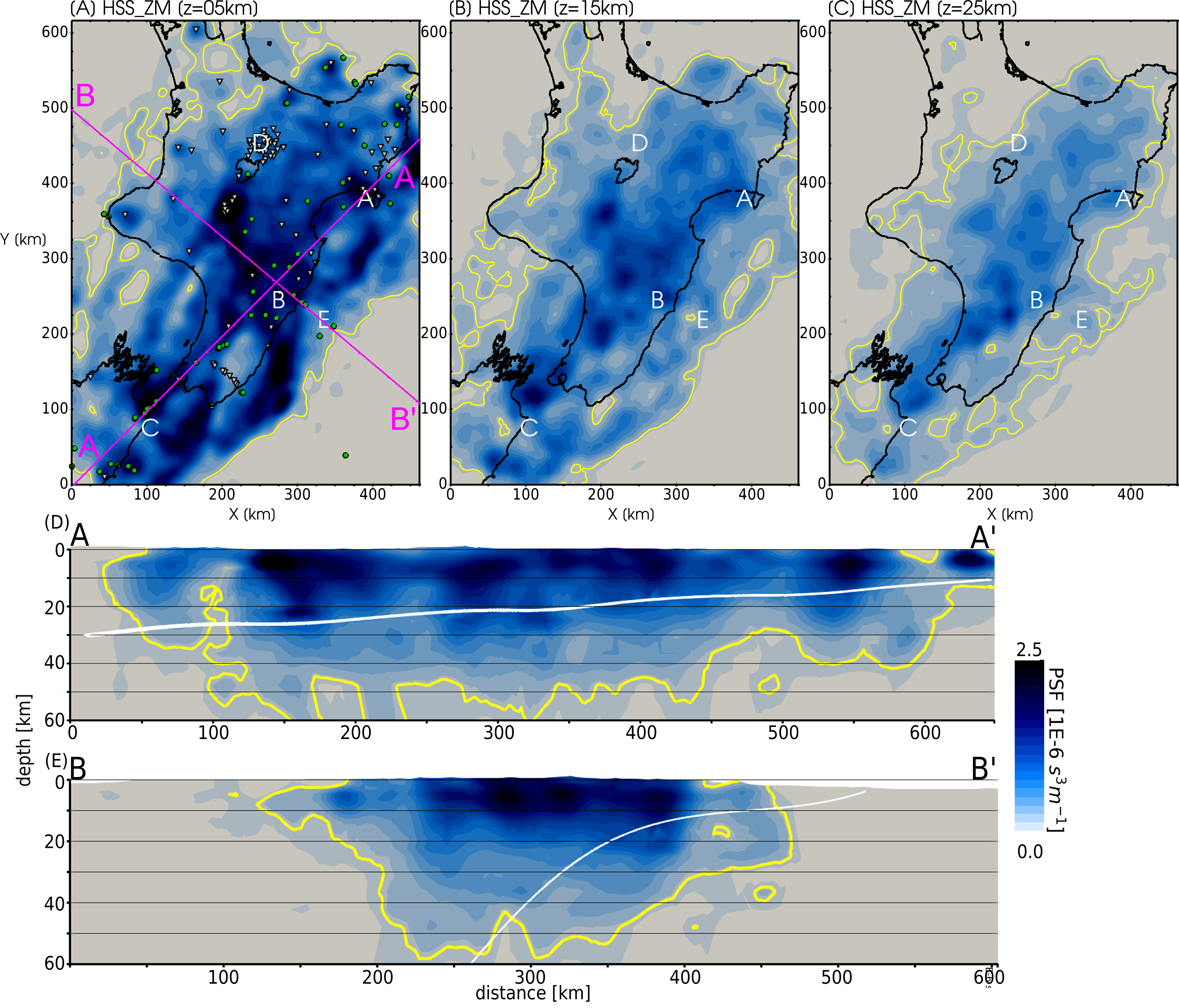
This is a 3D velocity model of the North Island of New Zealand derived using earthquake-based adjoint tomography.

Description

Name nz_atom_north_chow_etal_2021_vp+vs
Title New Zealand Adjoint TOMography velocity model (North Island)
Type 3-D Tomography Earth Model
Sub Type Shear-wave velocity (km/s) and Compressional-wave velocity (km/s)
Year 2021
EMC Data Revision r0.1 (revision history)
 
Short Description   This is a 3D velocity model of the North Island of New Zealand derived using earthquake-based adjoint tomography. The starting model is defined as the ray-based NZ-Wide2.2 Velocity Model from Eberhart-Phillips et al. (2021). To derive this velocity model, we iteratively improve fits between earthquake observations from New Zealand-based broadband seismometers and synthetically generated waveforms from spectral element simulations. The waveform bandpass of interest is 4-30s.
 
This velocity model defines the following quantities: Vp (km/s), Vs (km/s), density (kg/m3), Qp and Qs, however only Vp and Vs are updated during our inversion. The remaining quantities are defined by the starting velocity model.
 
Authors: Bryant Chow, Victoria University of Wellington, Wellington, New Zealand
GNS Science, Lower Hutt, New Zealand
(Now at University of Alaska Fairbanks)

Yoshihiro Kaneko, Department of Geophysics, Kyoto University, Kyoto, Japan

Carl Tape, Geophysical Institute, University of Alaska Fairbanks, Fairbanks, AK, USA

Ryan Modrak, Los Alamos National Laboratory, Los Alamos, NM, USA

Nick Mortimer, GNS Science, Dunedin, New Zealand

Stephen Bannister, GNS Science, Lower Hutt, New Zealand

John Townend, Victoria University of Wellington, Wellington, New Zealand
 
Contact Bryant Chow (bhchow@alaska.edu)
 
Previous Model
 
Reference Model NZ-Wide2.2 Velocity Model (Eberhart-Phillips et al.) Note: The provided reference model has been rotated and interpolated from its original format for use in our tomographic inversion. Additionally, this reference model encompasses a domain that is larger than the velocity model, but its values are only valid within the volume defined by the NZ ATOM North velocity model, stated explicitly in the Area section below.
 
Usage Notes   The geodetic datum of the original model is EPSG:32760 WGS 84/ UTM zone 60S. Two-dimensional latitude, longitude, coordinate variables in the netCDF 4 CLASSIC files for this model are expressed as a function of the UTM X and Y axis (see netCDF CF Metadata Conventions).
 
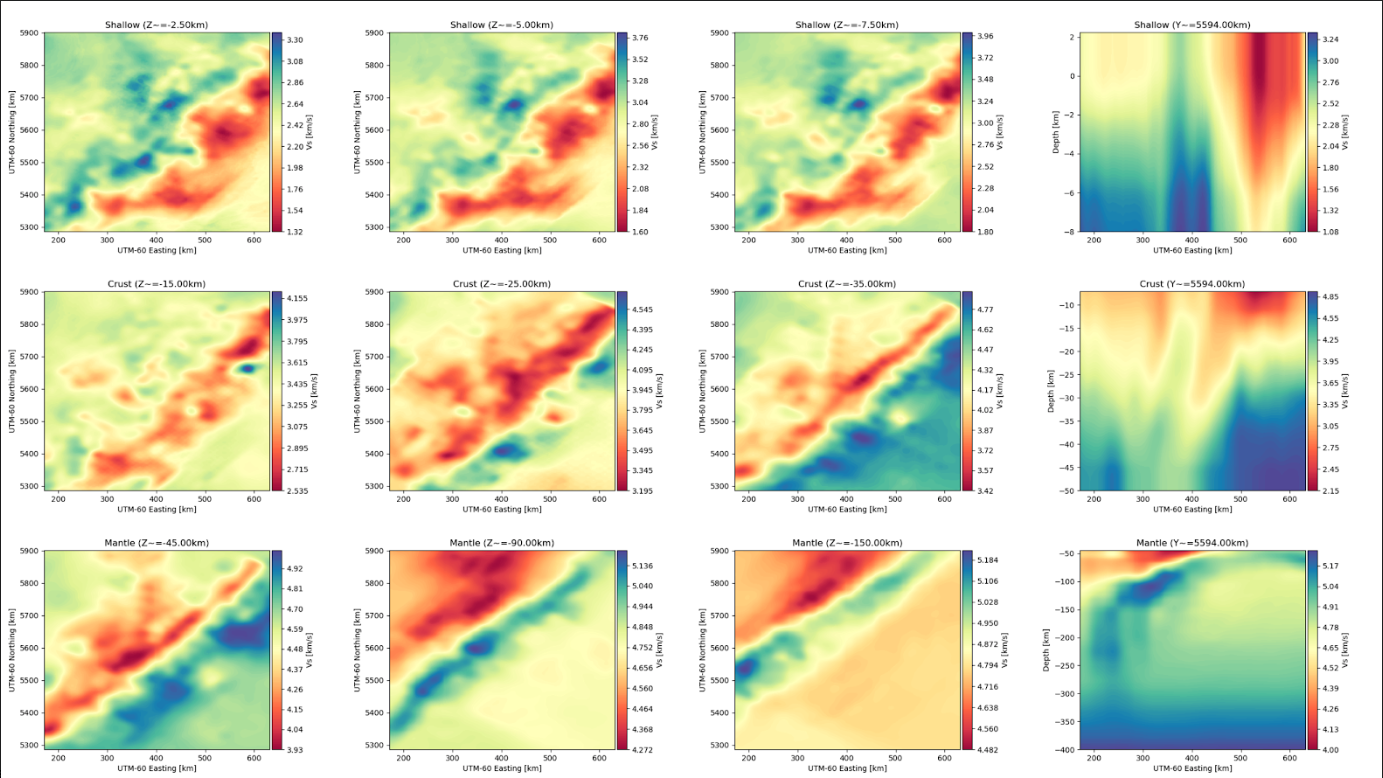
Data Files Description The velocity model is separated into three files covering overlapping depth ranges and with differing grid spacing:
  • shallow defines depths -2.25 to 8 km (BSL)
  • crust defines depths 7 to 50 km (BSL)
  • mantle defines depths 44 to 400 km (BSL)
Revision Notes Notes on NZATOM r0.1

Background
The New Zealand Adjoint TOmography Model (NZATOM) is a 3D velocity model derived from a full
waveform inversion using the numerical solver SPECFEM3D Cartesian (SPECFEM3D).

SPECFEM3D is a spectral-element solver, which solves the seismic wave equation on unstructured hexahedral meshes (deformed cubes). These GLL (Gauss-Lobatto-Legendre) models stretch and skew cubic elements to conform to interface boundaries (e.g., topography, moho topography), or coarsening layers, where elements increase in vertical or lateral size. These coarsening layers are used to decrease element sizes at depth, where seismic wavespeeds typically increase, allowing for less computational requirements for the same numerical resolution.

During the inversion procedure, two meshes with varying resolution were used in order to save computational expense. We call these two meshes coarse and fine. Both coarse and fine meshes had different element sizes and coarsening layer depths.

Due to decreasing resolution with depth, the final NZATOM model published on IRIS EMC is split into three overlapping blocks: shallow (-3–8km), crust (7–50km), mantle (44–400km)

Problem
The original model shows obvious numerical artefacts due to the interpolation of an unregular mesh onto a regular grid at various stages of the inversion workflow.
To obtain NZATOM in a file format usable by non-SPECFEM users, we needed to interpolate it onto a regular (XYZ) grid. The original method for doing so was to use a nearest-neighbor algorithm on the original
NZATOM GLL mesh to determine model values for a given uniform grid based on the nearest GLL point available. That is, for a given point r(x,y,z) in our regular grid, the program would find the nearest GLL
point and assign that to point r.

This method worked nominally for regular elements, but for skewed elements related to coarsening layers the nearest neighbor algorithm tended to create artefacts as certain points r began to show outlines of element boundaries as they passed through skewed elements.

During the inversion, this approach was also used to transfer our tomography model from the coarse to the fine mesh. Therefore the coarsening layers of the coarse mesh were imparted onto the fine mesh. Similarly, extracting the final velocity model imparted the coarsening layers of the fine mesh onto the published version
of NZATOM.
Figure 1
Fig. 1: Side-on view (Y-Z plane) of the NZATOM fine-resolution GLL model showing coarsening layers
at approximately 25km and 90km depths. These coarsening layers lead to artefacts from nearest-neighbor
interpolation of the original NZATOM model. Depths are shown in units of meters.
Artefacts Locations
Artefacts correspond to the coarsening layers of both the coarse and fine mesh:
  • Coarse Mesh Coarsening Layers: ~15–35km, ~75–125km
  • Fine Mesh Coarsening Layers: ~14–25km, ~65–100km
Solution
We interpolate affected model onto a regular mesh, smooth away artefacts, and re-extract onto regular grid.

To remove these artefacts from the underlying model, while avoiding adding any new additional artefacts, our approach was to start from a regularized GLL grid. That is, a GLL mesh with no topography, bathymetry, or coarsening layers, that shares an origin and domain with the original NZATOM GLL mesh.

We then take the NZATOM model present on IRIS EMC, in a regularized XYZ format and containing artefacts from the nearest neighbor approach, and interpolate this onto our new regularized mesh. The result is now a regular (cube-shaped elements) GLL mesh that has model values corresponding to the NZATOM model, and contains numerical artefacts.

We then apply a 2D Gaussian smoothing to the entire model. Smoothing coefficients for each smoothed model are provided in the following subsection. Smoothing coefficient values were determined through trial-and-error and visual inspection of the smoothed model, to determine if artefacts were sufficiently, without removing
real small-scale features in the models.

The smoothing procedure resulted in significant removal of the numerical artefacts, while perserving small-scale heterogeneities (~5km width). Although some artefacts can still be seen in the resulting model, they should not have significant affect on future applications of the model.

Workflow
  1. Generate regular GLL models with SPECFEM for: A) shallow, B) crust, C) mantle
  2. Interpolate NZATOM XYZ model from IRIS EMC onto meshes from (1)
  3. Smooth SPECFEM GLL models created in (2) using smoothing coefficients listed below
  4. Use nearest-neighbor to extract XYZ files from smoothed models of (3)
  5. Convert .xyz files to IRIS EMC netCDF format
Smoothing Coefficients
Shallow model (-2.25–8km depth):
  • Horizontal Half-Width = .5km
  • Vertical Half-width = .5km
Crustal model (7–50km depth):
  • Horizontal Half-Width = 3km
  • Vertical Half-width = 1km
Mantle model (44–400km depth):
  • Horizontal Half-Width = 4km
  • Vertical Half-width = 2km
Note: All parameters (vp, vs, rho, qp, qs) are smoothed Revised Model

The revised model was again derived by taking nearest-neighbor interpolation on a regular grid for each of the sub-models. Now that the underlying GLL model is regular, there are no artefacts that arise from this approach and the resulting XYZ models show smoothly varying values and no artefacting.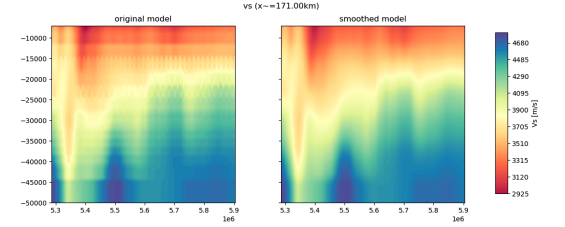
Figure 2
Fig. 2: Artefact removal, slice through Crust tomography model at X~=171km (Y-Z plane) for Vs in km/s.
Left: Original NZATOM model showing visible artefacts. Right: Revised (r0.1) NZATOM model smoothed
with a 2D Gaussian w/ a horizontal half-width of 3km, and a vertical half-width of 1km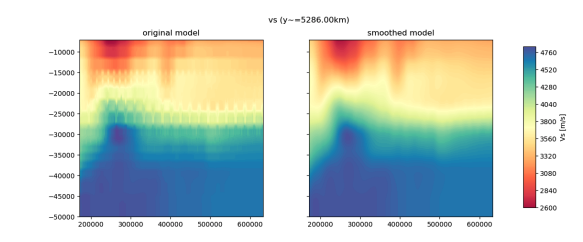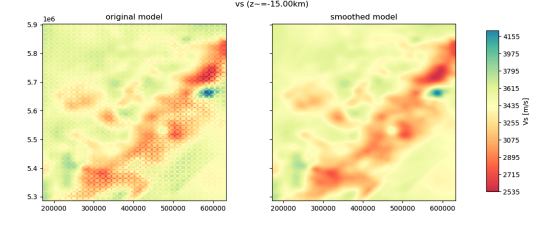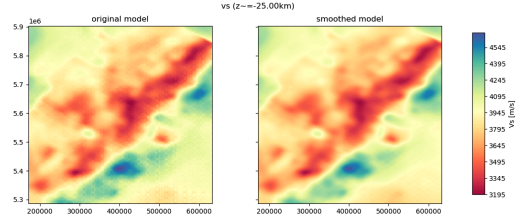

Figure 3
Fig 3: Same as Fig. 2 but for Y=5286km (X-Z plane)

Figure 4
Fig. 4: Same as Fig. 2 but for Z=15km BSL (X-Y plane)

Figure 5
Fig. 5: Same as Fig. 2 but for Z=25km BSL (X-Y plane)
Amplitudes

The smoothing procedure will have damped the largest amplitudes of the underlying model, resulting in slightly lower minimum and maximum amplitudes for all parameters.

Domain Bounds

Due to a new approach in interpolating the underlying model, the published revision has slightly different domain bounds as the original model (smaller). The grid spacing is kept the same as the original model.

Topography

The topography on the original NZATOM GLL model was defined by SRTM-30P, with no model values given for values in the air (above topography). Because the regular model published to IRIS EMC was given as a
regular cube, values in the air were extrapolated from the nearest point in the model. This newly revised model does the same, so Users are cautioned when querying model parameters above topography/bathymetry
depth values.
Model Download Please see the above Data Files Description and Usage Notes sections about these files.
Model files in netCDF 4 Classic format:
 
Depth Coverage -2.25 to 400.0 km (below earth surface)
 
Area North Island of New Zealand and the Hikurangi subduction zone Coordinate system: UTM 60S x-axis 17100,63100, y-axis 5286000, 5902000 Coordinate system: WGS84 latitude -42.6°, -36.9°, longitude 173.0°, 178.5°
 
Data Set Description Dataset includes seismic waveforms filtered at 4-30s period. Waveforms from 60 earthquakes recorded on up to 88 broadboad three-component seisimic stations, resulting in 1800 unique source-receiver pairs. Broadband stations include the following networks:
 
 

Depth slices and cross-sections
Depth slices and cross-sections (right column) through the NZ ATOM r0.1 Vs model in km/s. Model file identifier, and depth value or y-axis/northing value, are provided in the title of each sub-figure.

Comparisons
Comparisons of initial (M00; reference) and final (M28) shear-wave velocity (Vs) models at various depth slices. Columns represent initial model (M00; left), final model (M28; center), and net model update (ln(M28/M00); right). Rows represent depth slices at 5 km (top), 15 km (middle), and 25 km (bottom). Annotated letters A–E relate to notable velocity features not seen in the initial model. Note the differing color scales between rows and columns. Numerical artefacts related to mesh coarsening layers are visible in panels D, E, F, H, and I.

Zeroth moment test
Zeroth moment test: This volumetric field (HSS) approximates the sensitivity of the entire set of waveform measurements to perturbations in Vs structures. Darker colors represent higher relative sensitivity. The solid yellow lines outline a threshold sensitivity value. A) HSS at 5 km depth. Pink lines show surface traces of cross sections in (D) and (E). Earthquakes and receivers used in inversion are depicted as green circles and white inverted triangles. B) HSS at 15 km depth. C) HSS at 25 km depth. D) HSS A–A’ cross section to 60 km depth at 2x vertical exaggeration. E) HSS B–B’ cross section. White lines in cross sections correspond to the plate interface model of Williams et al. (2013).

Citations and DOIs

To cite the original work behind this Earth model:

  • Chow, Bryant, Yoshihiro Kaneko, Carl Tape, Ryan Modrak, Nick Mortimer, Stephen Bannister, and John Townend. “Strong upper-plate heterogeneity at the Hikurangi subduction margin (North Island, New Zealand) imaged by adjoint tomography.” Journal of Geophysical Research: Solid Earth, accepted Dec. 9, 2021, https://doi.org/10.1029/2021JB022865

To cite IRIS DMC Data Products effort:

  • Trabant, C., A. R. Hutko, M. Bahavar, R. Karstens, T. Ahern, and R. Aster (2012), Data Products at the IRIS DMC: Stepping Stones for Research and Other Applications, Seismological Research Letters, 83(5), 846–854, https://doi.org/10.1785/0220120032.

DOI for this EMC webpage: https://doi.org/10.17611/dp/emc.2021.nzatomnnorthvpvs.1

References

  • Chow, Bryant, Yoshihiro Kaneko, and John Townend. “Evidence for deeply-subducted lower-plate seamounts at the Hikurangi subduction margin: implications for seismic and aseismic behavior.” Journal of Geophysical Research: Solid Earth, accepted Dec. 28, 2021, https://doi.org/10.1029/2021JB022866
  • Chow, Bryant, Yoshihiro Kaneko, Carl Tape, Ryan Modrak, and John Townend. “An automated workflow for adjoint tomography—waveform misfits and synthetic inversions for the North Island, New Zealand.” Geophysical Journal International 223, no. 3 (2020): 1461-1480. https://doi.org/10.1093/gji/ggaa381
  • Eberhart-Phillips, Donna, Bannister, Stephen, Reyners, Martin, & Henrys, Stuart. (2020). New Zealand Wide model 2.2 seismic velocity and Qs and Qp models for New Zealand [Data set]. Zenodo. https://doi.org/10.5281/zenodo.3779523
  • Charles A. Williams, Donna Eberhart‐Phillips, Stephen Bannister, Daniel H. N. Barker, Stuart Henrys, Martin Reyners, Rupert Sutherland; Revised Interface Geometry for the Hikurangi Subduction Zone, New Zealand. Seismological Research Letters 2013; 84 (6): 1066–1073. https://doi.org/10.1785/0220130035

Credits

  • Model provided by Bryant Chow

Revision History

revision r0.1: uploaded June 8, 2023.
revision r0.0: uploaded December 17, 2021.

Timeline

2022-02-03
r0.0 online
2023-06-08
r0.1 online

Contact

Categories

Tags

EMC Earth Model Crust vs Vp Density Compressional-wave velocity adjoint tomography New Zealand

Related Content

These other pages were tagged similarly:

IRIS DMC has been certified as a trustworthy data repository by the CoreTrustSeal Standards and Certification Board
14:25:19 v.be17acbb