Summary
A 3‐D Shear Velocity Model of the Crust and Uppermost Mantle Beneath Alaska Including Apparent Radial Anisotropy.
Quicklinks
Description
| Name | Alaska-LFeng-2019_vsv_gamma |
| Title | A 3‐D Shear Velocity Model of the Crust and Uppermost Mantle Beneath Alaska Including Apparent Radial Anisotropy. |
| Type | 3-D Tomography Earth Model |
| Sub Type | Shear-wave velocity in km/s. Strength of radial anisotropy in %. |
| Year | 2019 |
| Short Description | A model of the 3‐D shear velocity structure of the crust and uppermost mantle beneath Alaska and its surroundings on a ~50‐km grid, including crustal and mantle radial anisotropy, based on seismic data recorded at more than 500 broadband stations. The model derives from a Bayesian Monte Carlo inversion of Rayleigh wave group and phase speeds and Love wave phase speeds determined from ambient noise and earthquake data. |
| Authors: | |
| Lili Feng | |
| USI Imaging | |
| Compagnie Générale de Géophysique (CGG) | |
| Michael Ritzwoller | |
| Department of Physics | |
| University of Colorado Boulder | |
| Boulder, CO, USA | |
| Previous Model | None |
| Reference Model | ak135 |
| Model Download | Alaska-LFeng-2019-vsv-gamma.nc (see metadata ), is the netCDF file for the model as a function of depth |
| Model Homepage | |
| Depth Coverage | 0 to 200 km |
| Area | Alaska and northwestern Canada (approx. 52°/72° latitude and -172°/-122° longitude) |
| Data Set Description | This dataset includes the absolute shear wave velocity structure with radial anisotropy of the crust and uppermost mantle beneath Alaska, derived from a joint inversion of the Rayleigh and Love wave data extracted from both ambient noise and earthquakes. The model is constructed with a Bayesian Monte Carlo inversion algorithm, providing reliable information about model uncertainties. |
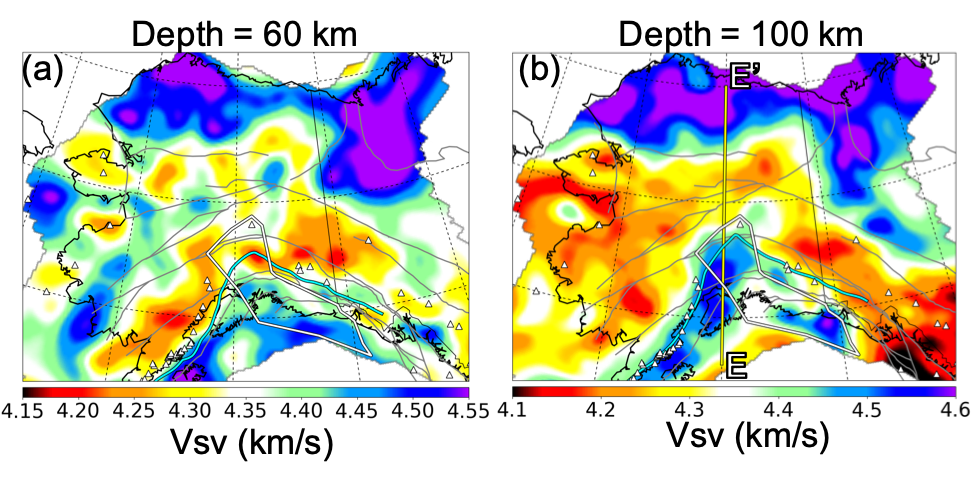
ranges in the mantle (central‐depth ± 3 km) with central‐depths of (a) 60 km
and (b) 100 km. Symbols are similar to Figure 11 in Feng & Ritzwoller (2019),
but additionally the cyan curve is the top edge of the subducting slab at each
map depth from the slab model of Jadamec and Billen (2010) and the lines E‐E′
identifies the vertical profile shown in Figure 21 in Feng & Ritzwoller (2019).
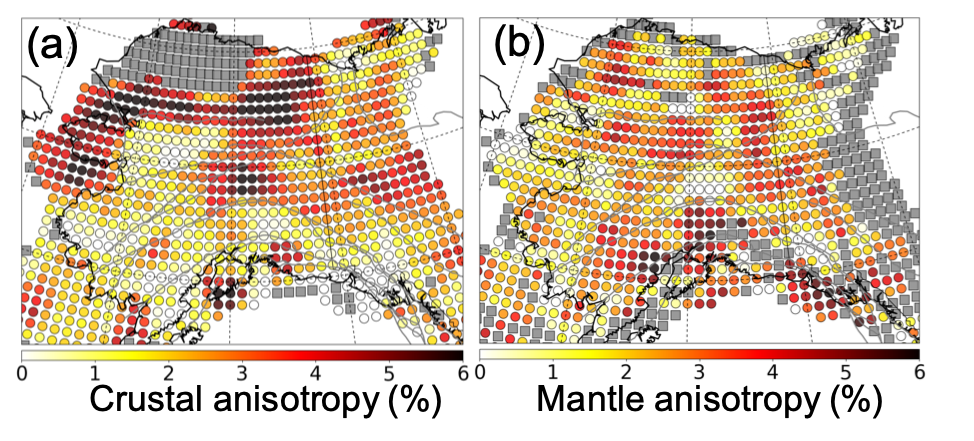
determined from the mean of the posterior distribution using both Rayleigh
and Love wave data. We consider estimates of γc to be indeterminate if the
standard deviation of the posterior distribution for γc is greater than 1.0% or
in the Colville Basin where we estimate γs rather than γc. Estimates of γm are
considered indeterminate if the standard deviation of the posterior distribution
is greater than 1.5%. The gray squares identify the indeterminate grid nodes.
This includes the whole of the Colville Basin for crustal anisotropy.
Citations and DOIs
To cite the original work behind this Earth model:
- Feng, L., and M.H.Ritzwoller, A 3-D shear velocity model of the crust and uppermost mantle beneath Alaska including apparent radial anisotropy, J. Geophys. Res. Solid Earth, 124, 19,468-10,497, https://doi.org/10.1029/2019JB018122, 2019.
To cite IRIS DMC Data Products effort:
- Trabant, C., A. R. Hutko, M. Bahavar, R. Karstens, T. Ahern, and R. Aster (2012), Data Products at the IRIS DMC: Stepping Stones for Research and Other Applications, Seismological Research Letters, 83(5), 846–854, https://doi.org/10.1785/0220120032.
DOI for this EMC webpage: https://doi.org/10.17611/dp/emcalaskalfeng2019
References
- Jadamec, M. A., & Billen, M. I. (2010). Reconciling surface plate motions with rapid three‐dimensional mantle flow around a slab edge. Nature, 465(7296), 338–341. https://doi.org/10.1038/nature09053
Credits
Model provided by Lili Feng
Timeline
- 2020-01-06
- online






